Every THING is Internet of Thing

Sorting Algorithms

 
  • Akhilesh Moghe
  • Dec 14, 2018

Visualization is the Best way to Learn Algorithms:

Courtesy: VISUALGO.NET

Selection Sort: O(n2)

  • Selection Sort maintains 2 sub-arrays in same array:
    • Sorted elements
    • Unsorted elements
  • In each iteration One element i.e. minimum is found and is swapped to the Sorted part of array.
  • In following implementation, there are 2 for() loops running for ‘arrSize’ i.e. n,
  • Time Complexity: O(n2)
  • Auxiliary Space Complexity: O(1)
    • As everything is accomplished in same array, no extra space required.

Illustration:

Selection Sort

Gist

Selection Sort for “Array of Strings”

Stable Selection Sort

  • A sorting algorithm is said to be stable: if the elements with Same Values/Keys retain Same Sequence in Output array as in Input array.
  • e.g.
    • Input : 4A 5 3 2 4B 1
    • Unstable Selection Sorting Output:
    • Output : 1 2 3 4B 4A 5
    • Stable Sorting Output:
    • Output : 1 2 3 4A 4B 5
  • Selection sort works by finding the minimum element and then inserting it in its correct position by swapping with the element which is in the position of this minimum element. This makes Selection Sort unstable.
  • Swapping might impact in pushing a key(let’s say A) to a position greater than the key(let’s say B) which are equal keys, which makes them out of the desired order.
  • In the above example 4A was pushed after 4B and after complete sorting this 4A remains after this 4B. Hence resulting in unstability.
  • Selection sort can be made Stable if instead of swapping, the minimum element is placed in its position pushing every element one step forward.

Gist

Insertion Sort: O(n2)

  • Time Complexity: O(n2)
  • Auxiliary Space: O(1)
  • Maximum Time to sort –> if elements are sorted in Reverse Order.
  • Minimum Time (Order of n) –> when elements are Already Sorted.
  • Algorithmic Paradigm: Incremental Approach
  • In-Place Sorting: Yes
  • Stable: Yes
  • Uses:
    • Used when number of elements are “Small”.
    • Also be useful when input Array is Almost Sorted, only few elements are misplaced in complete big array.
  • Analogy:
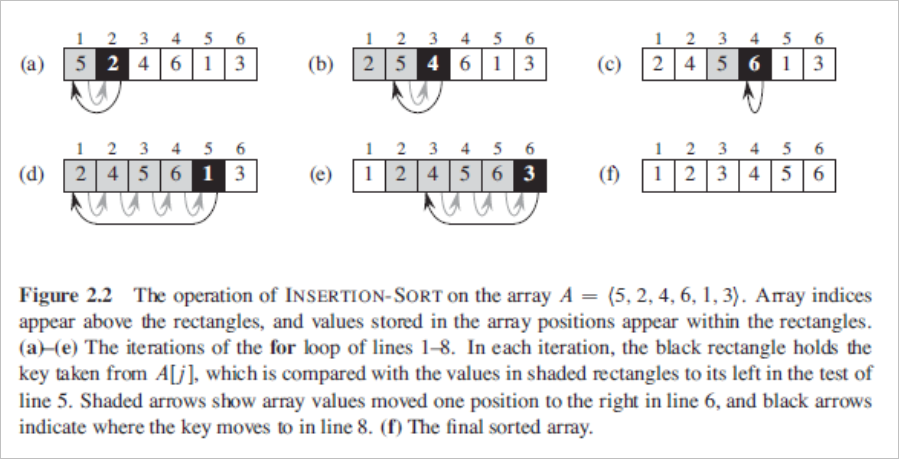
    • Insertion sort works the way many people sort a hand of playing cards.
    • We start with an empty left hand and the cards face down on the table.
    • We then remove one card at a time from the table and insert it into the correct position in the left hand.
    • To find the correct position for a card, we compare it with each of the cards already in the hand, from right to left,
    • At all times, the cards held in the left hand are sorted, and these cards were originally the top cards of the pile on the table.

Illustrations:

Insertion Sort

Psuedo Code:

Psuedo Code Psuedo Code Explaination

Gist

  • In normal Insertion Sort,
    • it takes O(n) comparisions(at nth iteration) in Worst Case.
    • We can reduce it to O(log n) by using Binary Search.
  • The algorithm as a whole still has a running Worst Case running time of O(n2), because of the series of swaps required for each insertion.

Gist

Bubble Sort: O(n2)

  • Sorting is done by: Comparing Adjacent items and Swapping them if they are not in order.
  • Algorithm repeatedly passes through array and Swaps element to make them in order.
  • When there is NO Swap in an iteration, that’s end of Sorting.
  • Optimization:
    • Usually Array is sorted in 2nd Last iteration itself, before the NO Swap iteration, but Bubble Sort still iterates again to reach NO Swap iteration.
    • The bubble sort algorithm can be optimized by observing that the n-th pass finds the n-th largest element and puts it into its final place. So, the inner loop can avoid looking at the last n − 1 items when running for the n-th time.
    • i.e., by avoiding the last iteration.
  • Time Complexity:
    • Worst and Average Case Time Complexity: O(n2
      • Worst case occurs when array is Reverse Sorted.
    • Best Case Time Complexity: O(n)
      • Best case occurs when array is already Sorted.
  • Auxiliary Space: O(1)
  • Boundary Cases:
    • Bubble sort takes minimum time (Order of n) when elements are already Sorted.
  • Sorting In Place, No extra Array: Yes

  • Stable Sorting: Yes

  • Applications:
    • As per Wikipedia, Bubble sort is not much useful in practical use-cases, rather Insertion sort performs better with same time complexity.
    • In-spiye of theis, in Computer Graphics, Bubble Sort is popular for its Capability to Detect a very Small Error (like swap of just two elements) in almost-Sorted arrays and fix it with just Linear Complexity (2n).

Illustrations:

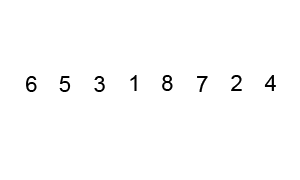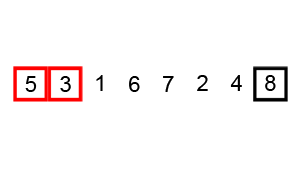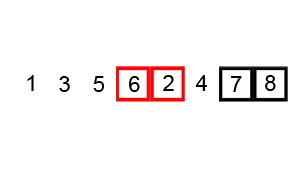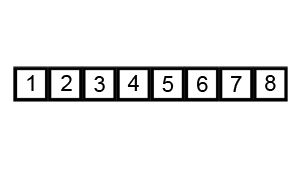
Bubble Sort gif

Gist

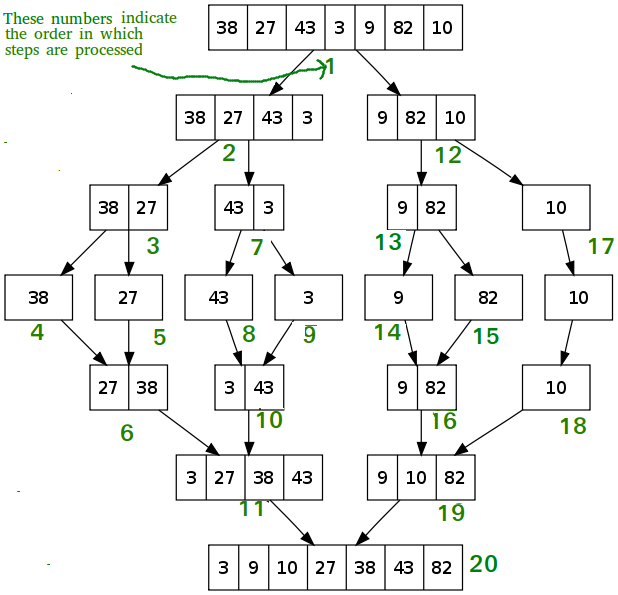
Merge Sort:

  • An efficient, general-purpose Algorithm
  • Comparison based Sorting Algorithm
  • Divide and Conquer Algorithm
    • It divides input array/List in two halves, calls itself for the two halves and then merges the two sorted halves.
  • Merge sort is often preferred for sorting a linked list.
    • The slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.

  • Basic Logic:

    MergeSort(arr[], l, r)
    If r > l
    1)    Find the middle point to divide the array into two halves:
           middle m = (l+r)/2
    2)    Call mergeSort for first half:
           Call mergeSort(arr, l, m)
    3)    Call mergeSort for second half:
           Call mergeSort(arr, m+1, r)
    4)    Merge the two halves sorted in step 2 and 3:
           Call merge(arr, l, m, r)\

  • Time Complexity: O(nLogn)
    • Time complexity of Merge Sort is O(nLogn) in all 3 cases (worst, average and best) as Merge Sort always Divides the array in Two Halves and take Linear Time to Merge Two Halves.
  • Auxiliary Space: O(n)
    • As we create 2 temporary Sub Arrays, totaling size of ‘n’.
  • Algorithmic Paradigm: Divide and Conquer
  • Sorting In Place: No
  • Stable: Yes

Illustrations:

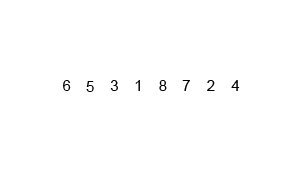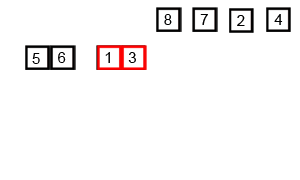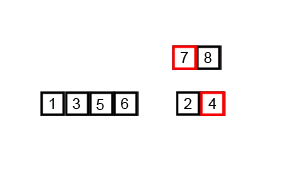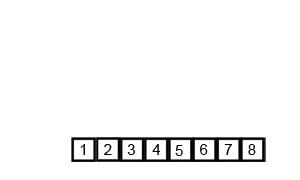
Merge-sort-example

Merge-Sort-Illustration

Comparison with other algorithms

  • Heapsort has the same time bounds as merge sort, it requires only Θ(1) auxiliary space instead of merge sort’s Θ(n).
  • Quicksort implementations generally outperform merge sort for sorting RAM-based arrays.
  • On the other hand, merge sort is a stable sort and is more efficient at handling slow-to-access sequential media.
  • Merge sort is often the best choice for sorting a linked list: in this situation it is relatively easy to implement a merge sort in such a way that it requires only Θ(1) extra space, and the slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.

Use-case

  • Merge sort is often the best choice for sorting a linked list.

Gist

References:
Search